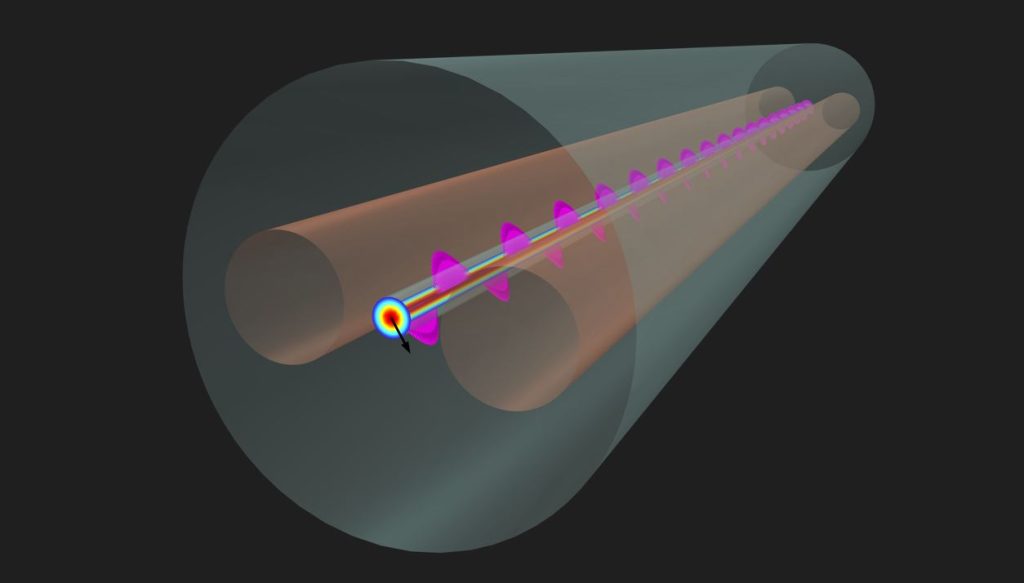
Le fibre ottiche sono una delle parti più importanti della moderna infrastruttura di comunicazione: costituiscono la spina dorsale di Internet e di altre reti digitali. Inoltre, le fibre ottiche sono indispensabili per le applicazioni industriali e mediche, come il taglio laser, la marcatura laser di componenti e prodotti e l’ablazione laser dei tumori.

Una fibra ottica può sembrare semplice perché la sua struttura fisica è costituita solo da un nucleo e da un rivestimento, ma richiede anche una sorgente luminosa per essere alimentata. La soluzione più comune per alimentare una fibra ottica è l’utilizzo di un laser. Di solito un raggio laser viene polarizzato linearmente con un orientamento specifico e può essere manipolato in vari modi utilizzando ottiche di polarizzazione come lamine quarto d’onda, celle di Pockels, isolatori di Faraday e finestre di Brewster.
Le imperfezioni comuni alle fibre ottiche causano una rotazione involontaria e indesiderata della polarizzazione, che spesso comporta una perdita di potenza durante l’erogazione del raggio laser. Ad esempio, è noto che qualsiasi materiale ottico presenta una leggera birifrangenza, ovvero indici di rifrazione diversi in diverse direzioni. Inoltre, il nucleo della fibra può essere leggermente ellittico o affusolato a causa di limiti di produzione, oppure può piegarsi durante l’uso. Complessità come queste rendono necessarie accurate simulazioni numeriche per lo sviluppo delle fibre ottiche.
Simulare la fibra
Per simulare le fibre ottiche, il primo passo è l’esecuzione di un’analisi 2D dei modi sulla sezione trasversale della fibra. Con questo tipo di analisi, è possibile prevedere quali modi possono esistere nella fibra in determinate condizioni. Il modo di uscita molto probabilmente non sarà lo stesso del modo di ingresso a causa delle imperfezioni della fibra e delle manipolazioni intenzionali del fascio descritte in precedenza. Per comprendere meglio come il modo si propaghi sulla lunghezza della fibra, sono necessarie simulazioni 3D.
Esistono diversi approcci per prevedere tale propagazione con la simulazione 3D, tra cui il metodo della propagazione del fascio (beam propagation method, BPM). Il BPM è utile perché numericamente è relativamente leggero, ma utilizza approssimazioni delle equazioni di Maxwell e di solito risolve per un campo scalare, anche se la luce è un campo vettoriale. Pertanto, tutti i fenomeni che richiedono una descrizione del campo vettoriale non possono essere simulati con questo metodo. Esistono BPM vettoriali, ma utilizzano anch’essi approssimazioni e sono numericamente onerosi e non facili da usare.
In alternativa, il Wave Optics Module, un componente aggiuntivo del software COMSOL Multiphysics®, è in grado di risolvere le equazioni di Maxwell con il beam envelope method (Rif. 1). Si tratta di un metodo basato sugli elementi finiti che può gestire in modo rigoroso componenti ottici estesi in 3D senza bisogno di una mesh eccessivamente fine o di qualsiasi approssimazione teorica, a condizione che sia soddisfatta una certa condizione: che la direzione di propagazione, rappresentata dal vettore d’onda, sia nota a priori con ragionevole precisione. Una fibra ottica soddisfa questa condizione perché il modo propagante è guidato dalla differenza di indice di rifrazione nella fibra, che è geometricamente predeterminata per dare una direzione di propagazione lungo l’estensione della fibra. Prima di effettuare la simulazione 3D completa, è necessario determinare la forma del fascio in direzione trasversale ai contorni di eccitazione e di uscita. A tal fine, l’analisi dei modi al contorno viene eseguita numericamente per ciascuno dei contorni di eccitazione e di uscita. Conosciuta anche come analisi dei modi trasversali, l’analisi dei modi al contorno è in grado di calcolare la forma vettoriale dei modi sui contorni e include tutte le componenti dei campi elettrici e magnetici. Una volta fatto questo e calcolato il numero d’onda trasversale, la costante di propagazione viene calcolata analiticamente e utilizzata come parametro di ingresso per la simulazione 3D. In molti casi, il calcolo è relativamente leggero, anche per le fibre lunghe, grazie all’efficienza del metodo dell’inviluppo del fascio e alla sua applicabilità alle fibre ottiche.
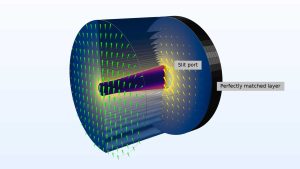
La Figura 2 mostra un caso estremizzato del problema tecnico descritto in precedenza: il nucleo di una fibra ottica è involontariamente rastremato (tapered) e la polarizzazione lineare iniziale ruota mentre il modo si propaga lungo la fibra. Questa simulazione è stata eseguita utilizzando un’interfaccia dedicata al beam envelope method all’interno del Wave Optics Module. Il fenomeno della rotazione della polarizzazione non può essere compreso con approssimazioni scalari, ma è di natura puramente vettoriale a causa dell’interazione tra il campo elettrico del laser e il materiale dei componenti ottici. Pertanto, per analizzare le fibre ottiche è necessaria una simulazione full-wave.
Fibre a mantenimento di polarizzazione
In una fibra ottica isotropa, i modi di ordine inferiore sono degeneri in due sensi. Questo significa che possono esistere due modi polarizzati linearmente e ortogonali a causa della simmetria circolare della sezione trasversale. Non esiste alcun meccanismo che impedisca a una polarizzazione dei due modi degeneri di accoppiarsi ad un altro modo con polarizzazione diversa in una fibra ottica isotropa. Qualsiasi deviazione dall’isotropia o dalla simmetria circolare del materiale può causare l’accoppiamento dei modi di polarizzazione.
Nelle fibre ottiche reali, a causa delle imperfezioni di fabbricazione o della birifrangenza del materiale, un piccolo accoppiamento di polarizzazione è inevitabile durante la propagazione. La il più piccolo accoppiamento diventa significativo, accumulandosi, quando il fascio si propaga su una lunga distanza. Pertanto, il piano di polarizzazione di una normale fibra ottica ruota.
Per mitigare il problema della rotazione della polarizzazione, si può ingegnerizzare una grande birifrangenza nella fibra. In questa situazione, l’accoppiamento di un modo di polarizzazione con un altro avviene raramente. Pertanto, è possibile realizzare una polarizzazione esclusiva lungo un asse scelto in modo preferenziale.

Tuttavia, non è possibile ottenere questo risultato con le fibre ordinarie, poiché non sono in grado di supportare una grande birifrangenza; è invece necessario utilizzare fibre a mantenimento di polarizzazione (Polarization-Maintaining, PM). Le fibre PM più comuni includono le fibre bow-tie, a cristallo fotonico e PANDA (ved. Figura 3). Le fibre PANDA e a cristallo fotonico sono ampiamente utilizzate per le telecomunicazioni, mentre le fibre bow-tie sono spesso impiegate per i sensori, come i sensori di torsione e i sensori giroscopici.
Come si può quindi realizzare intenzionalmente una grande birifrangenza? Per cominciare, le fibre PM vengono preparate con l’asse del nucleo (core rod) racchiuso da due assi di sollecitazione (stress rod) in un asse di rivestimento (cladding rod) e poi portato ad alta temperatura fino a raggiungere le dimensioni della fibra progettata. Una volta raffreddati, gli stress rod presentano una sollecitazione meccanica residua dovuta al contrasto del coefficiente di espansione termica. A questo scopo, gli stress rod sono tipicamente addizionati con B2O3. Per creare una birifrangenza, è possibile aggiungere un altro stress rod accanto al core rod, mentre gli stress rod hanno un diverso coefficiente di espansione termica (CTE) rispetto al core e al cladding.
La sollecitazione meccanica modifica significativamente gli indici di rifrazione dei materiali della fibra in modo anisotropo, a causa della mancanza di simmetria. L’asse lungo la linea con cui sono allineati gli stress rod è chiamato asse lento, mentre l’altro asse è chiamato asse veloce. In presenza di sollecitazioni meccaniche residue, lungo l’asse lento si forma una polarizzazione esclusiva.
Simulazione multifisica delle fibre PM
La progettazione, la caratterizzazione e la previsione delle prestazioni delle fibre PM richiedono l’uso di simulazioni multifisiche, in cui le analisi termiche e meccaniche possono essere risolte insieme alle analisi degli autovalori e alla simulazione elettromagnetica vettoriale. Questo tipo di modellazione e analisi può risultare complesso, ma il software COMSOL Multiphysics® basato sugli elementi finiti lo semplifica, poiché consente ai progettisti di fibre ottiche di:
- Combinare virtualmente qualsiasi fisica e risolverle insieme
- Modellare facilmente le proprietà anisotrope dei materiali che dipendono da variabili risolte in altre fisiche.
- Sfruttare il potente beam envelope method, che rende molto efficienti le simulazioni di fibre ottiche.
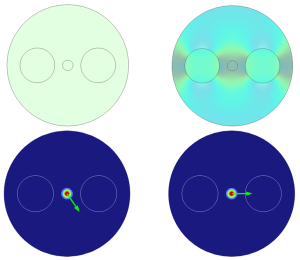
La Figura 4 mostra il risultato dell’analisi dei modi al contorno in 2,5 D eseguita in COMSOL® che confronta i casi con e senza sollecitazione meccanica.
Quando si caratterizza una fibra PM, si può eccitare un campo polarizzato in un piano tra i due assi di polarizzazione per misurare la lunghezza di beat. La lunghezza di beat delle tipiche fibre PM è dell’ordine dei millimetri, molto più corta di quella delle fibre ordinarie. La Figura 5 mostra una simulazione 3D full wave di una fibra PANDA con una polarizzazione lineare a 45 gradi, risultato di una polarizzazione circolare dell’asse lento.
Conclusioni
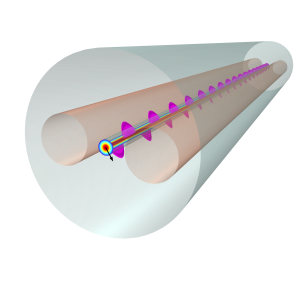
In questo articolo abbiamo discusso le simulazioni multifisiche full-wave di fibre ottiche, che sono concettualmente semplici ma richiedono tecniche di modellazione e simulazione sofisticate. L’efficiente beam envelope method per le simulazioni di fibre ottiche consente la simulazione 3D di lunghe sezioni di fibre. Questo metodo, utilizzato in combinazione con simulazioni multifisiche che includono l’espansione termica e le sollecitazioni meccaniche e che tengono conto delle proprietà anisotrope dei materiali, consente di analizzare gli effetti della birifrangenza.
Riferimenti
- Sjodin, “Wave Optics: Beam-Envelope Method Efficiently Analyzes Photonic Components,” Laser Focus World, 9 Nov. 2017; https://www.laserfocusworld.com/software-accessories/software/article/16548112/wave-optics-beamenvelope-method-efficiently-analyzes-photonic-components.
a cura di Yosuke Mizuyama – COMSOL